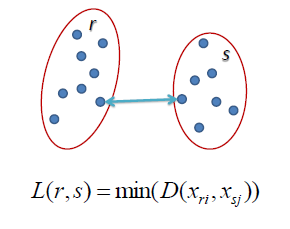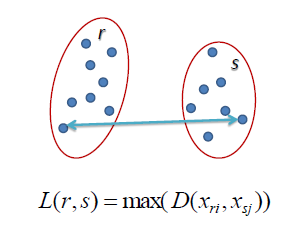| Map
> Data Science > Predicting the Future >
Modeling > Clustering
> Hierarchical |
|
|
|
|
|
|
Hierarchical Clustering
|
|
|
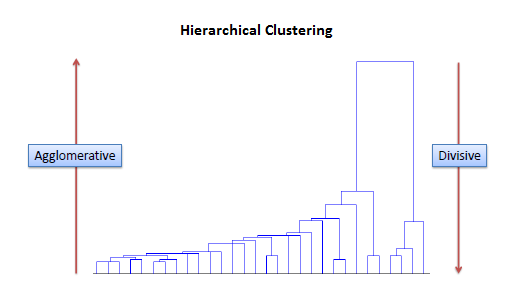
| Hierarchical clustering involves creating clusters that have a predetermined ordering from top to bottom. For example, all files and folders on the hard disk are organized in a hierarchy.
There are two types of hierarchical clustering, Divisive
and Agglomerative. |
|
|
|
|
|
|
| Divisive method |
|
|
| In divisive or top-down clustering method we assign all of the observations to a single
cluster and then partition the cluster to two least similar clusters using
a flat clustering method (e.g., K-Means).
Finally, we proceed recursively on each cluster until there is one cluster for each observation.
There is evidence that divisive algorithms produce more accurate hierarchies than
agglomerative algorithms in some circumstances but is conceptually more complex. |
|
|
| |
|
|
|
Agglomerative method
|
|
|
| In agglomerative or bottom-up clustering
method we assign each observation to its own
cluster. Then, compute the similarity (e.g., distance) between each of the
clusters and join the two most similar clusters. Finally, repeat steps 2 and 3 until there is only a single cluster left.
The related algorithm is shown below. |
|
|

|
|
|
| Before any clustering is performed, it is required to determine the proximity matrix containing the distance between each point using
a distance function. Then, the matrix is updated to display the distance between each cluster. The
following three methods differ in how the distance between each cluster is measured. |
|
|
| |
|
|
| Single Linkage |
|
|
| In single linkage hierarchical clustering, the distance between two clusters is defined as the
shortest distance between two points in each cluster. For example, the distance between clusters “r” and “s” to the left is equal to the length of the arrow between their two closest points. |
|
|
|
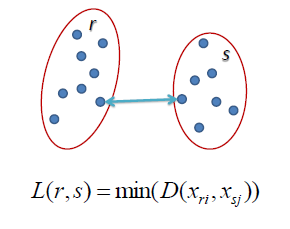
|
|
|
| Complete Linkage |
|
|
| In complete linkage hierarchical clustering, the distance between two clusters is defined as the
longest distance
between two points in each cluster. For example, the distance between clusters “r” and “s” to the left is equal to the length of the arrow between their two furthest points. |
|
|
|
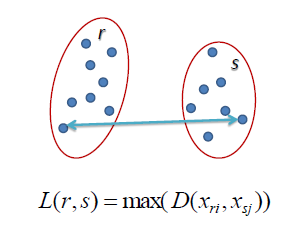
|
|
|
| Average Linkage |
|
|
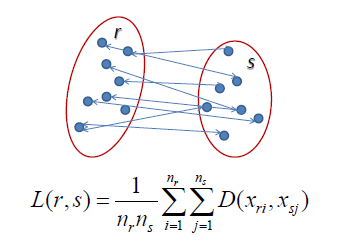
| In average linkage hierarchical clustering, the distance between two clusters is defined as the average
distance
between each point in one cluster to every point in the other cluster.
For example, the distance between clusters “r” and “s” to the left is equal to the average length each arrow between connecting the points of one cluster to the other. |
|
|
|
|
|
|
| |
|
|
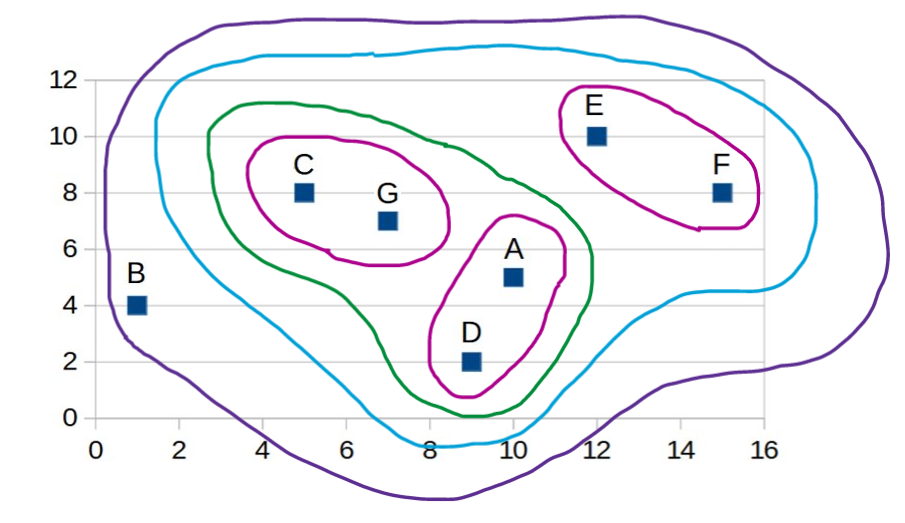
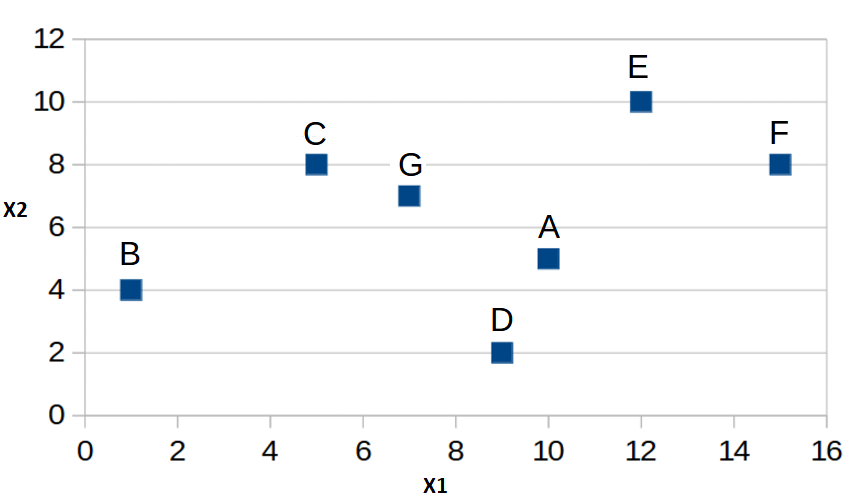
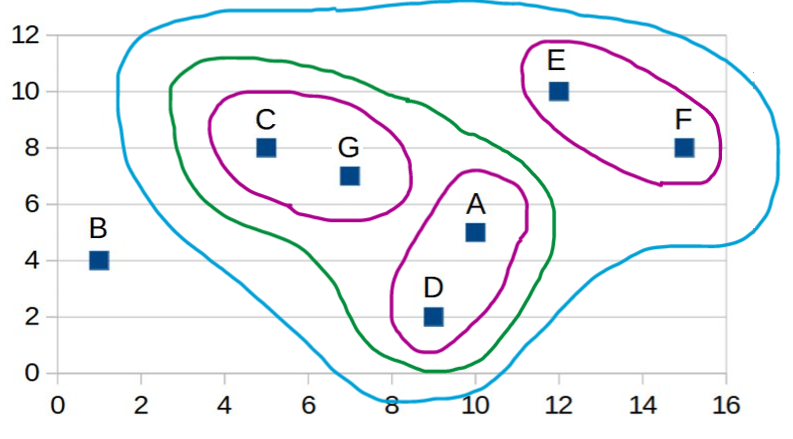
| Example: Clustering the following 7 data
points. |
|
|
| |
|
|
|
|
X1 |
X2 |
|
A |
10 |
5 |
|
B |
1 |
4 |
|
C |
5 |
8 |
|
D |
9 |
2 |
|
E |
12 |
10 |
|
F |
15 |
8 |
|
G |
7 |
7 |
|
|
|
|
|
|
|
| |
|
|
| Step 1: Calculate distances between all data
points using Euclidean distance function. The shortest distance is
between data points C and G. |
|
|
|
|
A |
B |
C |
D |
E |
F |
|
B |
9.06 |
|
|
|
|
|
|
C |
5.83 |
5.66 |
|
|
|
|
|
D |
3.16 |
8.25 |
7.21 |
|
|
|
|
E |
5.39 |
12.53 |
7.28 |
14.42 |
|
|
|
F |
5.83 |
14.56 |
10.00 |
16.16 |
3.61 |
|
|
G |
3.61 |
6.71 |
2.24 |
8.60 |
5.83 |
8.06 |
|
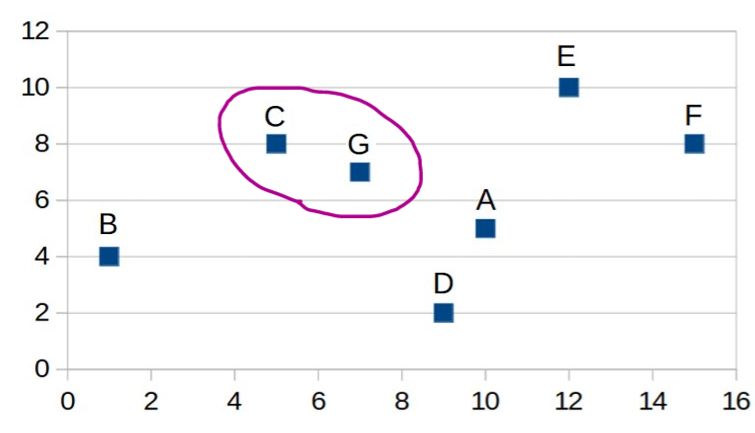
|
|
|
|
| |
|
|
| Step 2: We use "Average Linkage"
to measure the distance between the "C,G" cluster and other data
points. |
|
|
|
|
A |
B |
C,G |
D |
E |
|
B |
9.06 |
|
|
|
|
|
C,G |
4.72 |
6.10 |
|
|
|
|
D |
3.16 |
8.25 |
6.26 |
|
|
|
E |
5.39 |
12.53 |
6.50 |
14.42 |
|
|
F |
5.83 |
14.56 |
9.01 |
16.16 |
3.61 |
|
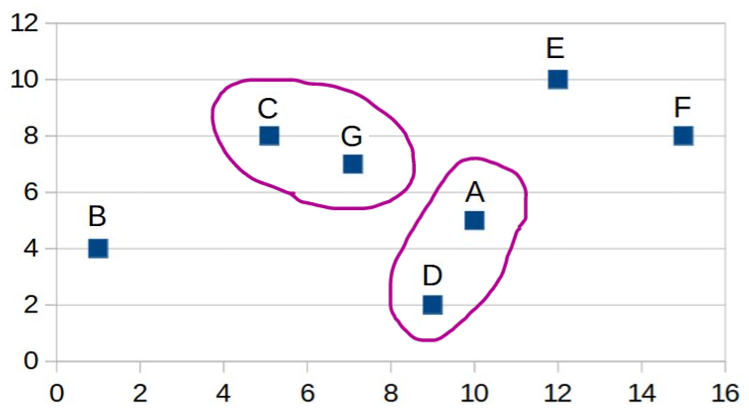
|
|
|
|
| |
|
|
| Step 3: |
|
|
|
|
A,D |
B |
C,G |
E |
|
B |
8.51 |
|
|
|
|
C,G |
5.32 |
6.10 |
|
|
|
E |
6.96 |
12.53 |
6.50 |
|
|
F |
7.11 |
14.56 |
9.01 |
3.61 |
|
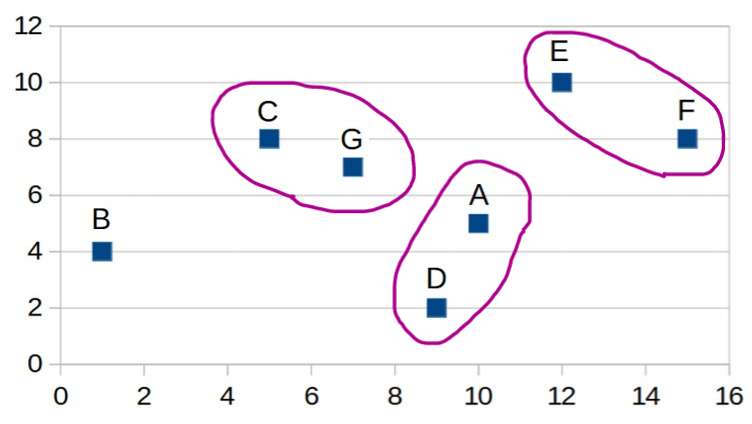
|
|
|
|
| |
|
|
| Step 4: |
|
|
|
|
A,D |
B |
C,G |
|
B |
8.51 |
|
|
|
C,G |
5.32 |
6.10 |
|
|
E,F |
6.80 |
13.46 |
7.65 |
|
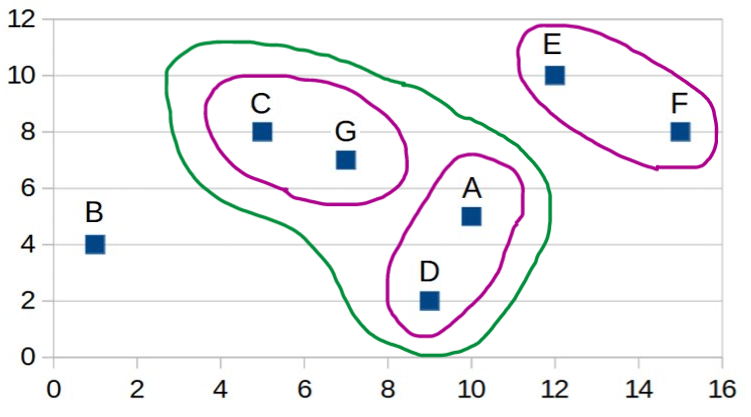
|
|
|
|
| |
|
|
| Step 5: |
|
|
|
|
A,D,C,G |
B |
|
B |
6.91 |
|
|
E,F |
6.73 |
13.46 |
|
|
|
|
|
| |
|
|
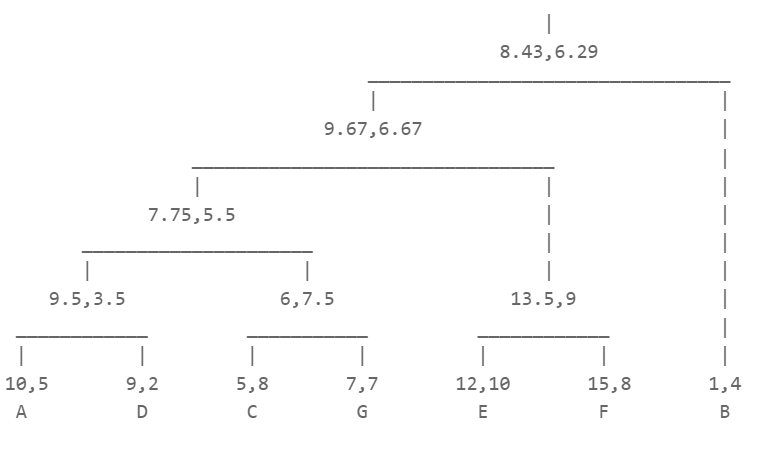
| Step 6: |
|
|
|
|
|
|
| |
|
|
| Final dendrogram: |
|
|
|
|
|
|
| |
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|