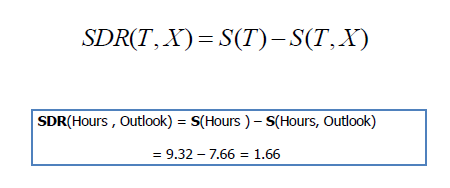| Map
> Data Science > Predicting the Future >
Modeling > Regression
> Decision Tree |
|
|
|
|
|
|
Decision Tree -
Regression
|
|
|
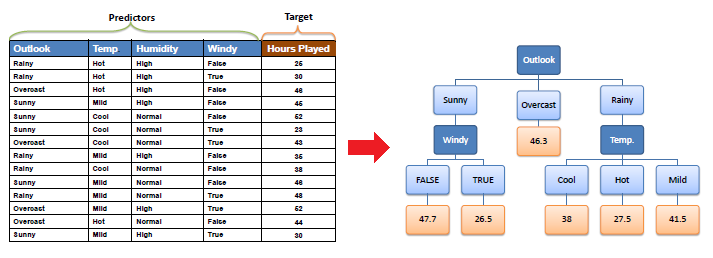
| Decision tree builds regression or classification
models in the form of a tree structure. It breaks down a dataset into smaller and smaller subsets while at the same time an associated decision tree is incrementally developed.
The final result is a tree with decision nodes and leaf nodes.
A decision node (e.g., Outlook) has two or more branches (e.g., Sunny,
Overcast and Rainy), each representing values for the attribute tested.
Leaf node (e.g., Hours Played) represents a decision on the numerical
target. The topmost decision node in a tree which corresponds to
the best predictor called root node. Decision trees can
handle both categorical and numerical data. |
|
|
|
|
|
|
| |
|
|
Decision Tree Algorithm
|
|
|
| The core algorithm for building decision trees
called ID3 by J. R. Quinlan which employs a top-down, greedy search through the space of possible
branches with no backtracking. The ID3 algorithm can be used to construct
a decision tree for regression by replacing Information Gain with Standard
Deviation Reduction. |
|
|
|
|
|
| Standard Deviation |
|
|
| A decision tree is built top-down from a root node and involves partitioning the data into subsets that contain instances with similar
values (homogenous). We use standard deviation to calculate the homogeneity of a
numerical sample.
If the numerical sample is completely homogeneous its standard deviation is zero. |
|
|
|
|
|
|
| a) Standard deviation for one
attribute: |
|
|
|

|
|
|
|
|
|
|
-
Standard Deviation (S) is
for tree building (branching).
-
Coefficient of Deviation (CV)
is used to decide when to stop branching. We can use Count (n)
as well.
-
Average (Avg) is the value
in the leaf nodes.
|
|
|
|
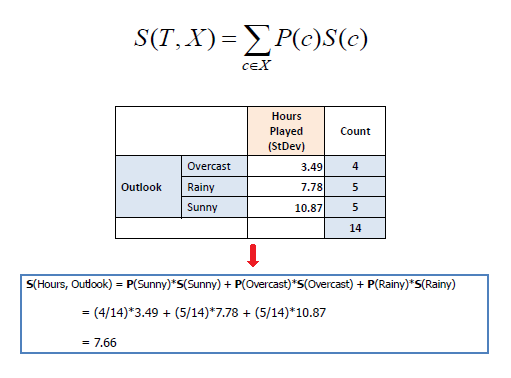
b) Standard deviation for two attributes
(target and predictor): |
|
|
|
|
|
|
| |
|
|
| Standard Deviation Reduction |
|
|
| The standard deviation reduction is based on the decrease in
standard deviation after a dataset is split on an attribute.
Constructing a decision tree is all about finding attribute that returns
the highest standard deviation reduction (i.e., the most homogeneous branches). |
|
|
|
|
|
|
|
Step 1: The standard deviation of the target is
calculated. |
|
|
|
|
|
|
|
Standard deviation (Hours
Played) = 9.32 |
|
|
|
|
|
|
|
Step 2:
The dataset is then split on the different attributes. The standard
deviation for each branch is calculated. The resulting standard deviation is subtracted from the
standard deviation before the split.
The result is the standard deviation reduction. |
|
|
|
|
|
|
|
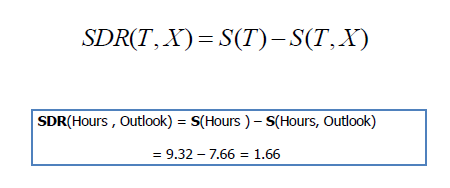
|
|
|
|
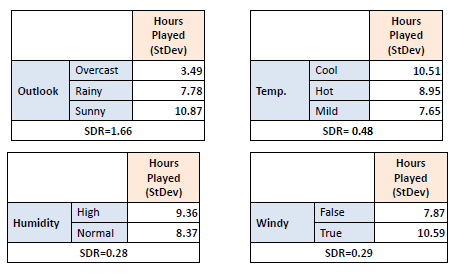
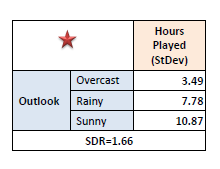
Step 3: The attribute with the largest
standard deviation reduction is chosen for the decision node. |
|
|
|
|
|
|
|
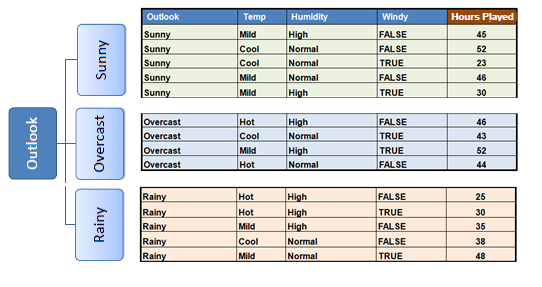
Step 4a: The dataset is divided based on the
values of the selected attribute. This process is run recursively on the non-leaf branches, until all data is processed. |
|
|
|
|
|
|
|
In practice, we need some termination criteria. For
example, when coefficient of deviation (CV) for a branch becomes smaller than a certain
threshold (e.g., 10%) and/or when too few instances (n) remain
in the branch (e.g., 3). |
|
|
|
|
|
|
|
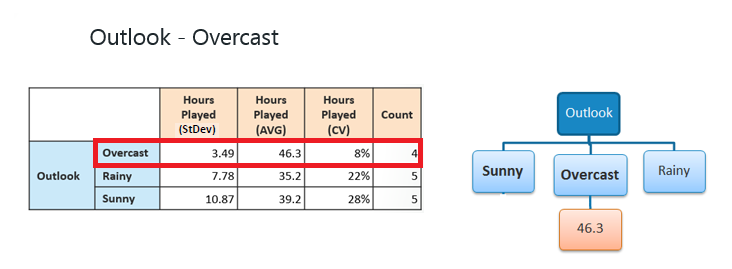
Step 4b: "Overcast" subset does not
need any further splitting because its CV (8%) is less than the threshold
(10%). The related leaf node gets the average of the "Overcast"
subset. |
|
|
|
|
|
|
|
|
|
|
|
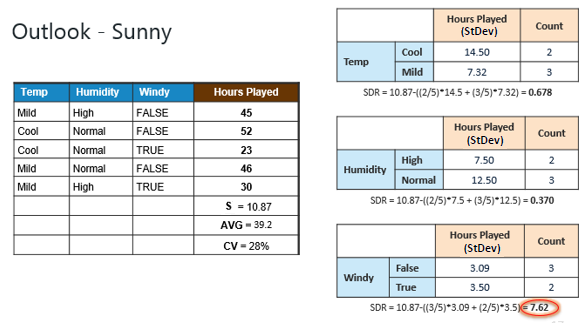
Step 4c: However, the "Sunny" branch
has an CV (28%) more than the threshold (10%) which needs further
splitting. We select "Temp" as the best best node after
"Outlook" because it has the largest SDR. |
|
|
|
|
|
|
|
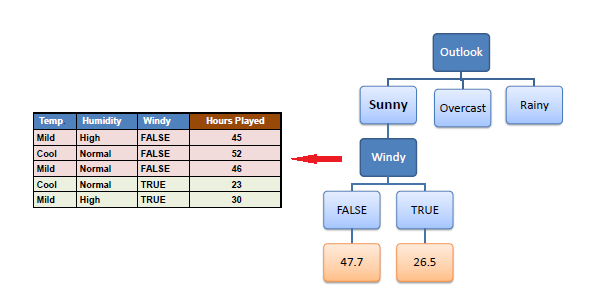
Because the number of data points for both branches
(FALSE and TRUE) is equal or less than 3 we stop further branching and
assign the average of each branch to the related leaf node. |
|
|
|
|
|
|
|
|
|
|
|
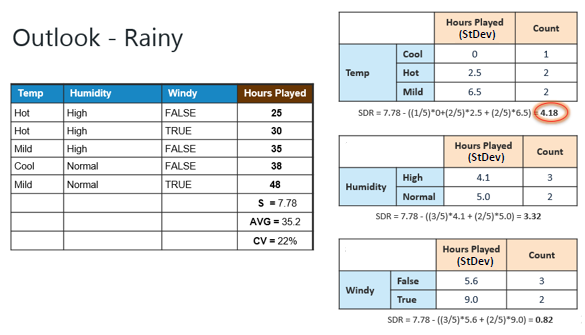
Step 4d: Moreover, the "rainy"
branch has an CV (22%) which is more than the threshold (10%). This branch
needs further splitting. We select "Temp" as the best best node
because it has the largest SDR. |
|
|
|
|
|
|
|
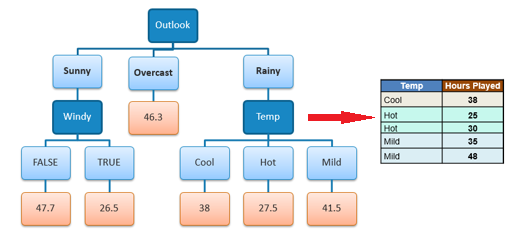
Because the number of data points for all three
branches (Cool, Hot and Mild) is equal or less than 3 we stop further
branching and assign the average of each branch to the related leaf node. |
|
|
|
|
|
|
|
|
|
|
|
When the number of instances is more than one at a
leaf node we calculate the average as the final value for the
target. |
|
|
| |
|
|
|
|
|
|
| |
|
|
 Try to invent a new algorithm to construct a decision
tree from data using MLR instead of average at the
leaf node.
Try to invent a new algorithm to construct a decision
tree from data using MLR instead of average at the
leaf node. |
|
|
|
|
|