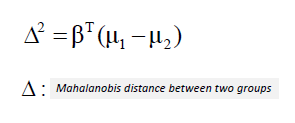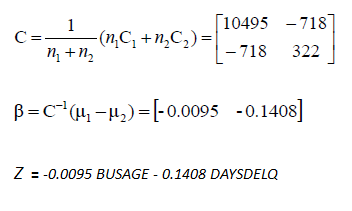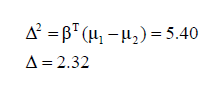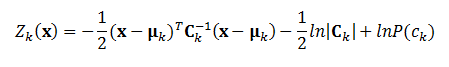Map > Data Science > Predicting the Future > Modeling > Classification > Linear Discriminant Analysis
Linear Discriminant Analysis
Linear Discriminant Analysis (LDA) is a classification method originally developed in 1936 by R. A. Fisher. It is simple, mathematically robust and often produces models whose accuracy is as good as more complex methods.
Algorithm
LDA is based upon the concept of searching for a linear combination of variables (predictors) that best separates two classes (targets). To capture the notion of separability, Fisher defined the following score function.
Given the score function, the problem is to estimate the linear coefficients that maximize the score which can be solved by the following equations.
One way of assessing the effectiveness of the discrimination is to calculate the Mahalanobis distance between two groups. A distance greater than 3 means that in two averages differ by more than 3 standard deviations. It means that the overlap (probability of misclassification) is quite small.
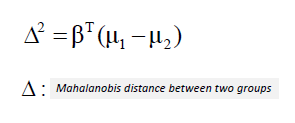
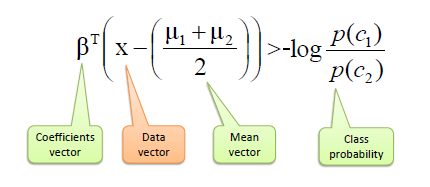
Finally, a new point is classified by projecting it onto the maximally separating direction and classifying it as C1 if:
Example:
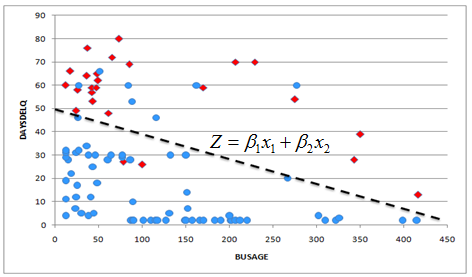
Suppose we received a dataset from a bank regarding its small business clients who defaulted (red square) and those that did not (blue circle) separated by delinquent days (DAYSDELQ) and number of months in business (BUSAGE). We use LDA to find an optimal linear model that best separates two classes (default and non-default).
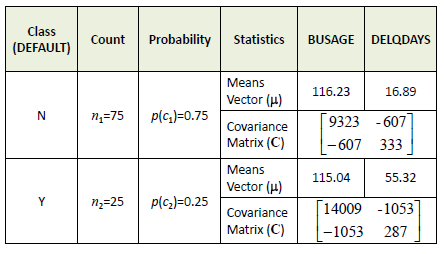
The first step is to calculate the mean (average) vectors, covariance matrices and class probabilities.
Then, we calculate pooled covariance matrix and finally the coefficients of the linear model.
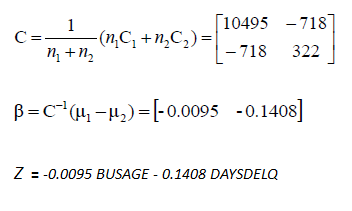
A Mahalanobis distance of 2.32 shows a small overlap between two groups which means a good separation between classes by the linear model.
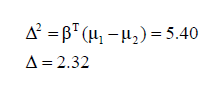
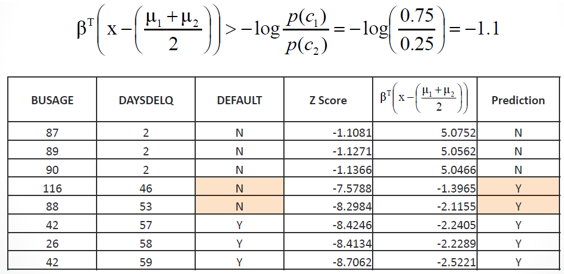
In the following table, we calculate Z score using the above Z equation. However, a score by itself cannot be used for predicting an outcome. We also need the equation in column 5 to choose Class N or Y. We predict Class N if the calculated value is bigger than -1.1 otherwise Class Y. As it is shown below, the LDA model made two errors.
Predictors Contribution
A simple linear correlation between the model scores and predictors can be used to test which predictors contribute significantly to the discriminant function. Correlation varies from -1 to 1, with -1 and 1 meaning the highest contribution but in different directions and 0 means no contribution at all.
Quadratic Discriminant Analysis (QDA)
QDA is a general discriminant function with a quadratic decision boundaries which can be used to classify datasets with two or more classes. QDA has more predictability power than LDA but it needs to estimate the covariance matrix for each classes.
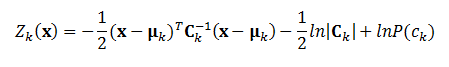
where Ck is the covariance matrix for the class k (-1 means inverse matrix), |Ck| is the determinant of the covariance matrix Ck, and P(ck) is the prior probability of the class k. The classification rule is simply to find the class with highest Z value.
Try to invent a real time LDA classifier. You should be able to add or remove data and variables (predictors and classes) on the fly.