Unsupervised Binning
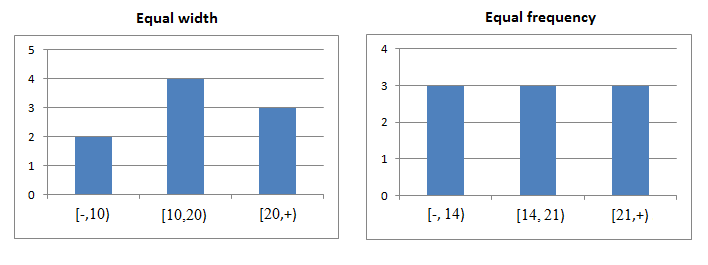
1- Equal Width Binning
w = (max-min)/k
min+w, min+2w, ... , min+(k-1)w
2- Equal Frequency Binning

3- Other Methods
- Rank: The rank of a number is its size relative to other values of a numerical variable. First, we sort the list of values, then we assign the position of a value as its rank. Same values receive the same rank but the presence of duplicate values affects the ranks of subsequent values (e.g., 1,2,3,3,5). Rank is a solid binning method with one major drawback, values can have different ranks in different lists.
- Quantiles (median, quartiles, percentiles, ...): Quantiles are also very useful binning methods but like Rank, one value can have different quantile if the list of values changes.
- Math functions: For example, FLOOR(LOG(X)) is an effective binning method for the numerical variables with highly skewed distribution (e.g., income).
| Exercise |