| Map
> Data Science > Predicting the Future >
Modeling >
Classification > Decision Tree |
|
|
|
|
|
|
Decision Tree -
Classification
|
|
|
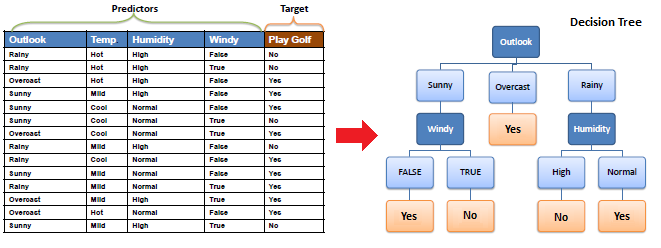
| Decision tree builds classification or
regression models in the form of a tree structure. It breaks down a dataset into smaller and smaller subsets while at the same time an associated decision tree is incrementally developed.
The final result is a tree with decision nodes and leaf nodes.
A decision node (e.g., Outlook) has two or more branches (e.g., Sunny,
Overcast and Rainy).
Leaf node (e.g., Play) represents a classification or decision. The topmost decision node in a tree which corresponds to
the best predictor called root node. Decision trees can
handle both categorical and numerical data. |
|
|
|
|
|
|
|
|
|
|
| |
|
|
Algorithm
|
|
|
| The core algorithm for building decision trees
called ID3 by J. R. Quinlan which employs a top-down, greedy search through the space of possible
branches with no backtracking. ID3 uses Entropy and Information Gain to
construct a decision tree. In ZeroR model there is no predictor, in OneR model we try to find the single best predictor, naive Bayesian includes all predictors using Bayes' rule and
the independence assumptions between predictors but decision
tree includes all predictors with the dependence assumptions between
predictors. |
|
|
|
|
|
| Entropy |
|
|
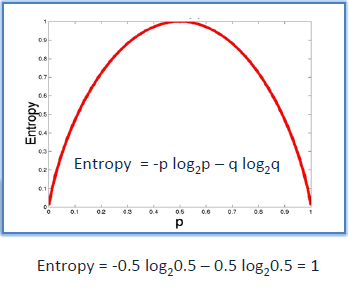
| A decision tree is built top-down from a root node and involves partitioning the data into subsets that contain instances with similar
values (homogenous). ID3 algorithm uses entropy to calculate the homogeneity of a sample.
If the sample is completely homogeneous the entropy is zero and if the
sample is an equally divided it has entropy of one. |
|
|
| |
|
|
|
|
|
|
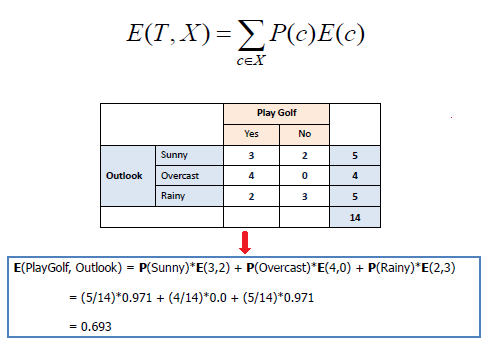
| To build a decision tree, we need to
calculate two types of entropy using frequency tables as follows: |
|
|
|
|
|
| a) Entropy using the frequency table of
one attribute: |
|
|
|
|
|
|
|
b) Entropy using the frequency table of two
attributes: |
|
|
|
|
|
|
| |
|
|
| Information Gain |
|
|
| The information gain is based on the decrease in entropy after a dataset is split on an attribute.
Constructing a decision tree is all about finding attribute that returns
the highest information gain (i.e., the most homogeneous branches). |
|
|
|
|
|
|
|
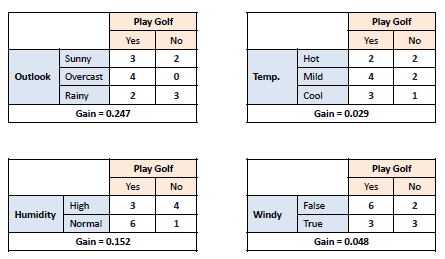
Step 1: Calculate entropy of the target. |
|
|
|
|
|
|
|
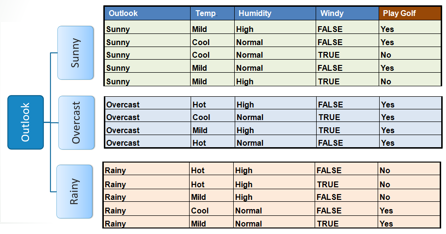
Step 2:
The dataset is then split on the different attributes. The entropy for each branch is calculated. Then it is added proportionally, to get total entropy for the
split. The resulting entropy is subtracted from the entropy before the split.
The result is the Information Gain, or decrease in entropy. |
|
|
|
|
|
|
|
|
|
|
|
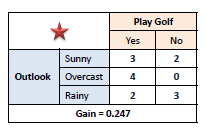
Step 3: Choose attribute with the largest
information gain as the decision node, divide the dataset by its branches
and repeat the same process on every branch. |
|
|
|
|
|
|
|
|
|
|
|
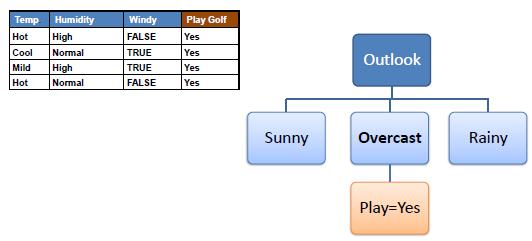
Step 4a:
A branch with entropy of 0 is a leaf node. |
|
|
|
|
|
|
|
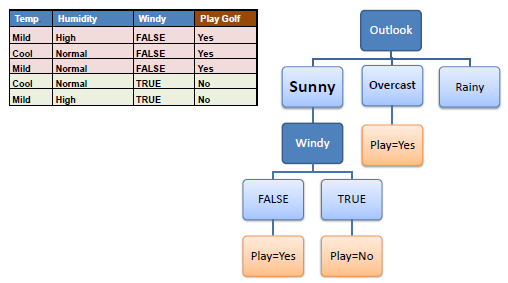
Step 4b:
A branch with entropy more than 0 needs further splitting. |
|
|
|
|
|
|
|
Step 5:
The ID3 algorithm is run recursively on the non-leaf branches, until all data is classified. |
|
|
|
|
|
|
|
|
|
|
Decision Tree to Decision Rules
|
|
|
| A decision tree can easily be
transformed to a set of rules by mapping from the root node to the leaf
nodes one by one. |
|
|
|
|
|
|
|
|
|
|
|
|
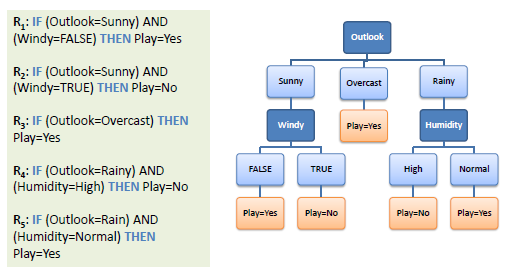
Decision Trees - Issues
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
Try to invent a new algorithm to construct a decision
tree from data using Chi2
test.
|
|
|
|
|
|
