| Map
> Data Science > Predicting the Future >
Modeling > Classification
> Decision Tree > Overfitting |
|
|
|
|
|
|
Decision Tree -
Overfitting
|
|
|
Overfitting is a significant practical difficulty for decision tree
models and many other predictive models. Overfitting happens when the learning algorithm continues
to develop
hypotheses that reduce training set error at the cost of an
increased test set error. There are several approaches to avoiding
overfitting in building decision trees. |
|
|
|
|
|
- Pre-pruning that stop growing the tree earlier, before it
perfectly classifies the training set.
- Post-pruning that allows the tree to perfectly
classify the training set, and then post prune the tree.
|
|
|
| Practically, the second approach of post-pruning
overfit trees is more successful because it is not easy to precisely
estimate when to stop growing the tree. |
|
|
|
|
|
| The important step of tree pruning is to
define a criterion be used to determine the correct final tree size using
one of the following methods: |
|
|
- Use a distinct dataset from the training set
(called validation set), to evaluate the effect of post-pruning nodes from the tree.
- Build the tree by using the training set, then apply a statistical test to estimate whether
pruning or expanding a particular node is likely to produce an improvement beyond the training set.
- Error estimation
- Significance testing (e.g., Chi-square test)
- Minimum Description Length principle : Use an explicit measure of the complexity for encoding the training
set and the decision tree, stopping growth of the tree when this encoding size
(size(tree) + size(misclassifications(tree)) is minimized.
|
|
|
|
The first method is the most common approach. In this approach, the available data are separated into two sets of examples: a training set, which is used to
build the decision tree, and a validation set, which is used to evaluate the impact of pruning
the tree. The second method is also a common approach. Here, we explain
the error estimation and Chi2 test.
|
|
|
|
|
|
|
|
Post-pruning using Error estimation
|
|
|
| Error estimate for a sub-tree is weighted sum of error
estimates for all its leaves. The error estimate (e)
for a node is: |
|
|
|

|
|
|
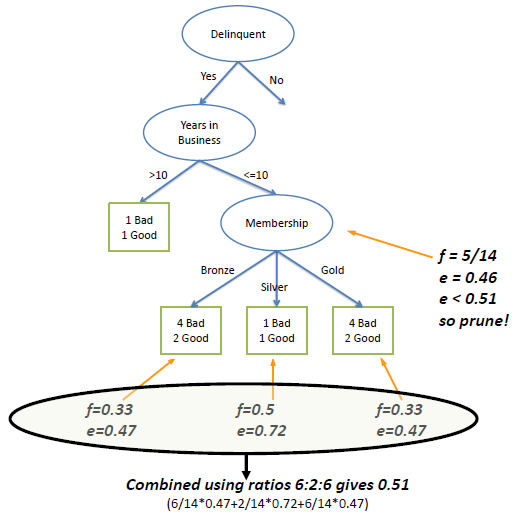
| In the following example we set Z to 0.69
which is equal to a confidence level of 75%. |
|
|
|
|
|
|
| The error rate at the parent node is 0.46 and since the error rate
for its children (0.51) increases with the split, we do not want to keep the children. |
|
|
| |
|
|
| Post-pruning using Chi2 test |
|
|
| In Chi2
test we construct the corresponding frequency table and calculate the
Chi2 value and its probability. |
|
|
|
|
|
|
| |
Bronze |
Silver |
Gold |
| Bad |
4 |
1 |
4 |
| Good |
2 |
1 |
2 |
|
|
|
|
Chi2 =
0.21 Probability =
0.90 degree of freedom=2 |
|
|
| |
|
|
| If we require that the probability has to be less than
a limit (e.g., 0.05), therefore we decide not to split the node. |
|
|
|
|
|
|
|
|

